The Unit Circle
Instructor Katherine Cliff
The Unit Circle
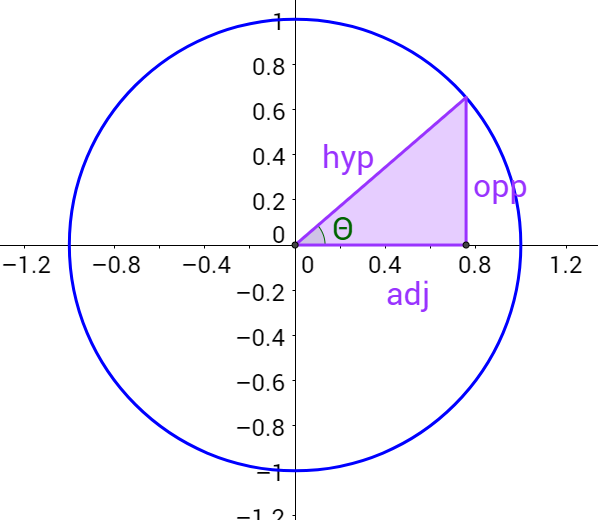
- The Unit Circle is a circle centered at the origin, (0,0), with radius 1 unit.
- \(\cos(\theta) = \frac{x}{1} = x\)
- \(\sin(\theta) = \frac{y}{1} = y\)
This gives us a new way to think about sine and cosine!

- Before: \(\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}\), using a reference angle \(\theta\) in a right triangle.
- Now: \(\sin(\theta) =\) y-coordinate associated with the point on the unit circle where the terminal side of angle \(\theta\) intersects the circle.
This gives us a new way to think about sine and cosine!

- Before: \(\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}\), using a reference angle \(\theta\) in a right triangle.
- Now: \(\cos(\theta) =\) x-coordinate associated with the point on the unit circle where the terminal side of angle \(\theta\) intersects the circle.
When we think about sine and cosine as coordinates on the unit circle…
we rename them the Circular Functions.
Quadrantal angles
\(\cos(0^\circ) = 1\),
\(\cos(90^\circ) = 0\),
\(\cos(180^\circ) = -1\),
\(\cos(270^\circ) = 0\),
\(\cos(360^\circ) = 1\),
\(\sin(0^\circ) = 0\)
\(\sin(90^\circ) = 1\)
\(\sin(180^\circ) = 0\)
\(\sin(270^\circ) = -1\)
\(\sin(360^\circ) = 0\)
Quadrantal angles
\(\cos(0) = 1\),
\(\cos\left(\frac{\pi}{2}\right) = 0\),
\(\cos(\pi) = -1\),
\(\cos\left(\frac{3\pi}{2}\right) = 0\),
\(\cos(2\pi) = 1\),
\(\sin(0) = 0\)
\(\sin\left(\frac{\pi}{2}\right) = 1\)
\(\sin(\pi) = 0\)
\(\sin\left(\frac{3\pi}{2}\right)= -1\)
\(\sin(2\pi) = 0\)
The Pythagorean Identity

According to the Pythagorean Theorem
\[x^2+y^2 = 1^2.\]
But, we have seen that \(x = \cos(\theta)\) and \(y = \sin(\theta)\) on the unit circle, so
\[(\cos(\theta))^2 + (\sin(\theta))^2 = 1,\]
which is commonly notated as
\[\cos^2(\theta) + \sin^2(\theta) = 1.\]
This is known as the Pythagorean Identity, and it is true for any angle \(\theta\).
Example:
Use the Pythagorean identity to find the value of \(\sin(\theta)\) if \(\cos(\theta) = \frac{2}{7}\) and the terminal side of angle \(\theta\) in standard position falls in QIV.
Example:
Use the Pythagorean identity to find the value of \(\cos(\theta)\) if \(\sin(\theta) = \frac{2}{5}\) and the terminal side of angle \(\theta\) in standard position falls in QII.
Building the Unit Circle
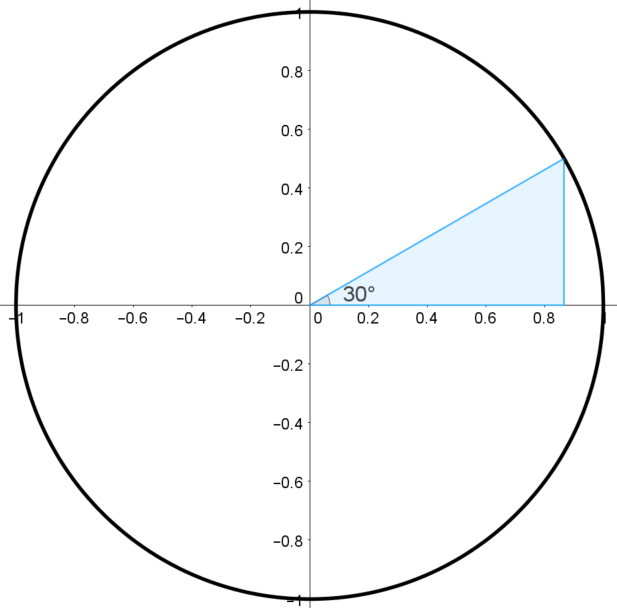
Building the Unit Circle
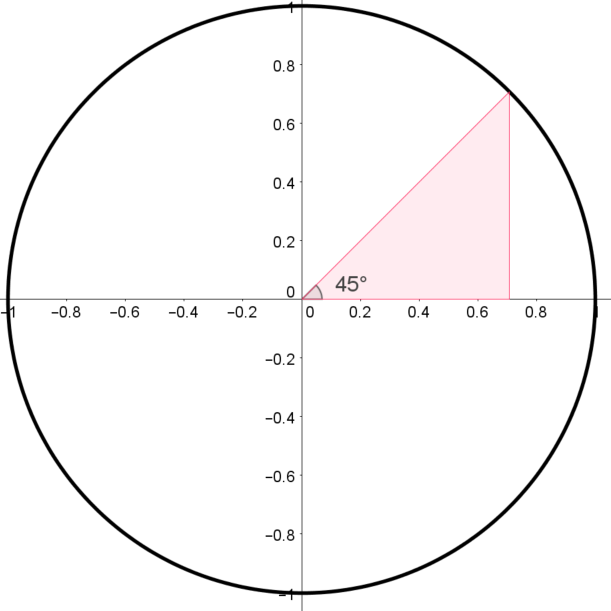
Building the Unit Circle
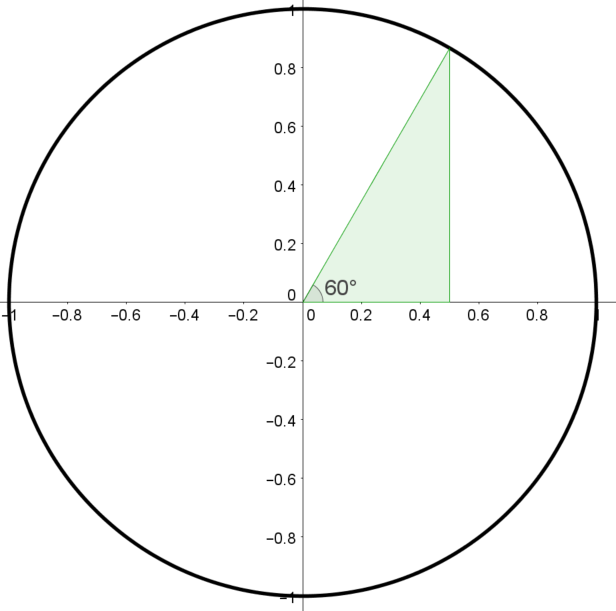
What we have so far
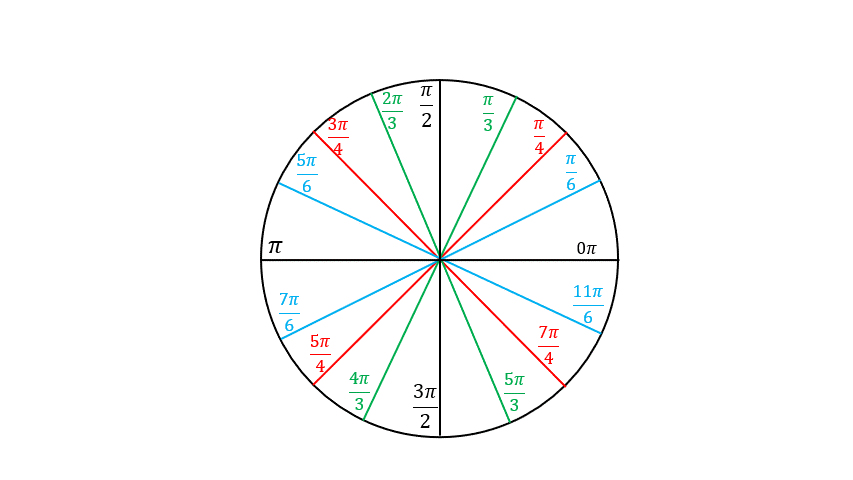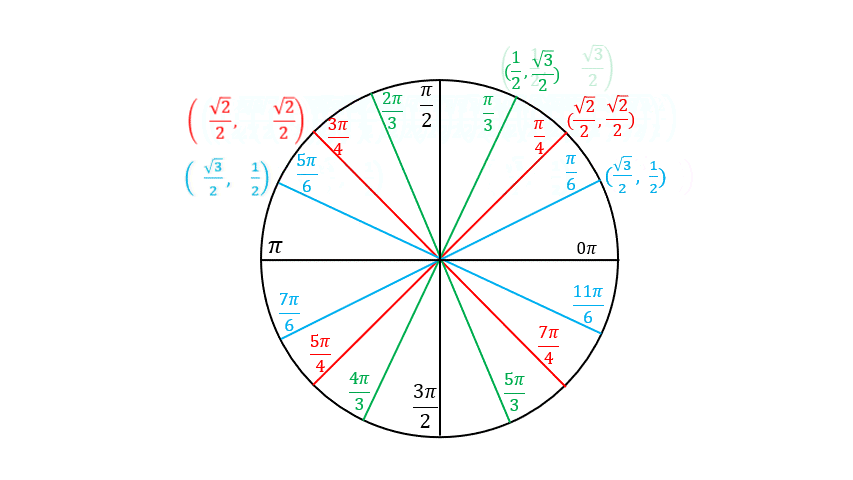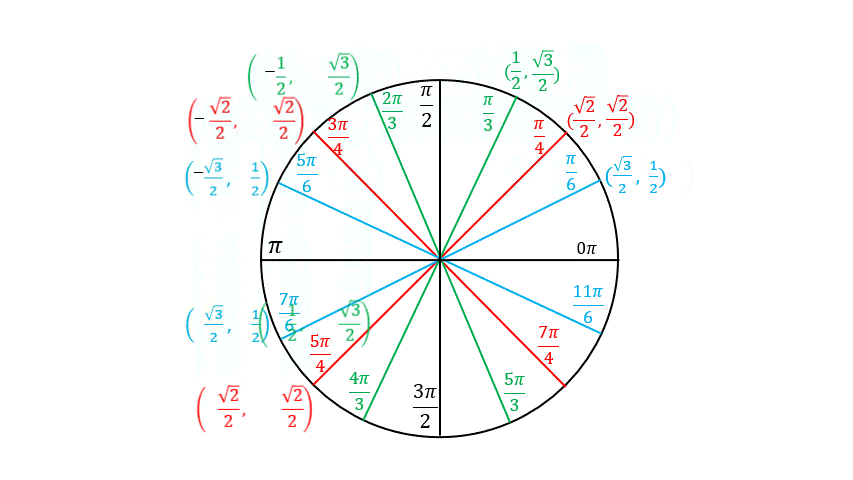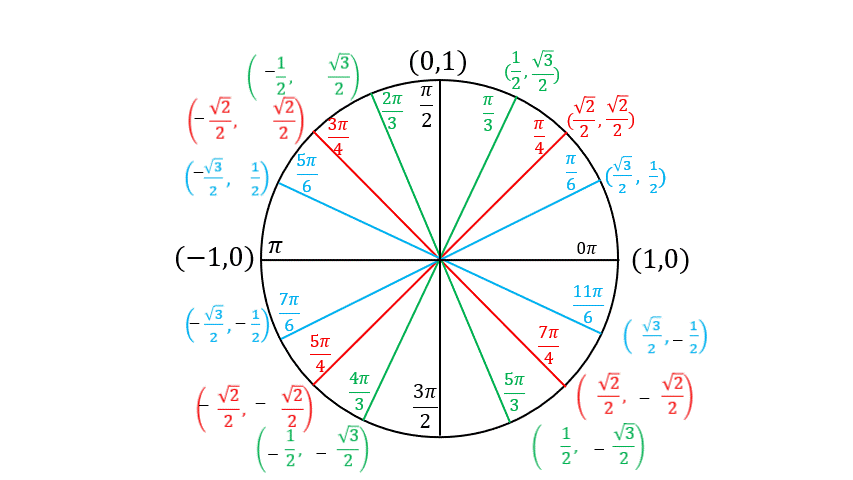
The Unit Circle
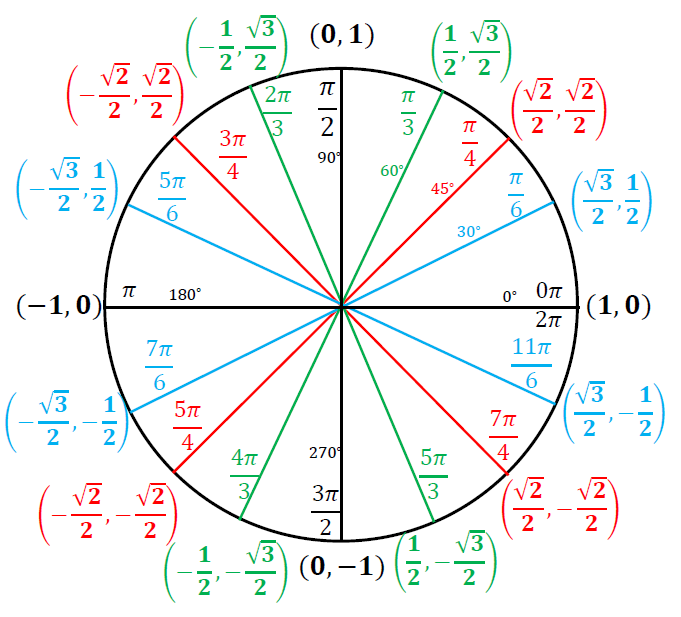
Example: Evaluate each expression using the unit circle
\[\cos\left(\frac{7\pi}{6}\right)\]
\[\sin\left(\frac{3\pi}{4}\right)\]
Example: Evaluate each expression using the unit circle
\[\sin\left(\frac{4\pi}{3}\right)\]
\[\cos\left(\frac{3\pi}{2}\right)\]
Example: Evaluate each expression using the unit circle
\[\cos\left(\frac{13\pi}{6}\right)\]
\[\sin\left(-\frac{2\pi}{3}\right)\]
The other trig functions…

Example: Evaluate each expression using the unit circle
\[\csc\left(\frac{5\pi}{3}\right)\]
\[\tan\left(\frac{2\pi}{3}\right)\]
Example: Evaluate each expression using the unit circle
\[\sec\left(\frac{\pi}{2}\right)\]
\[\cot\left(\frac{4\pi}{3}\right)\]
Memorization Tips
The angles
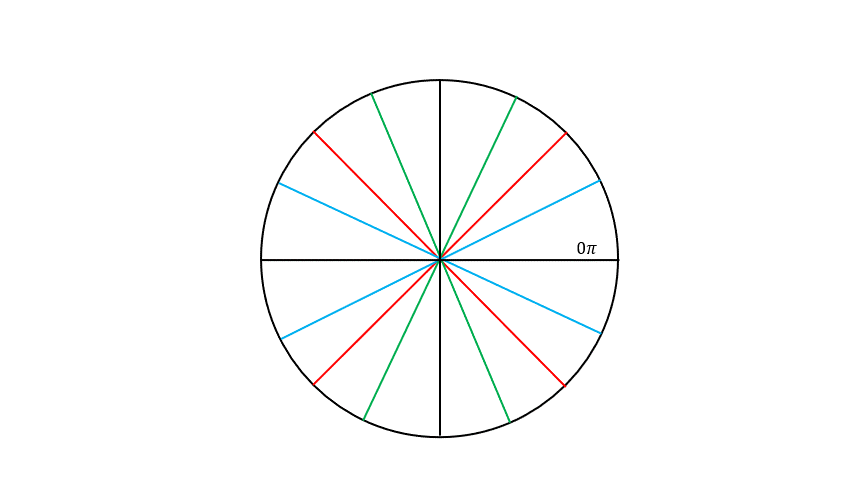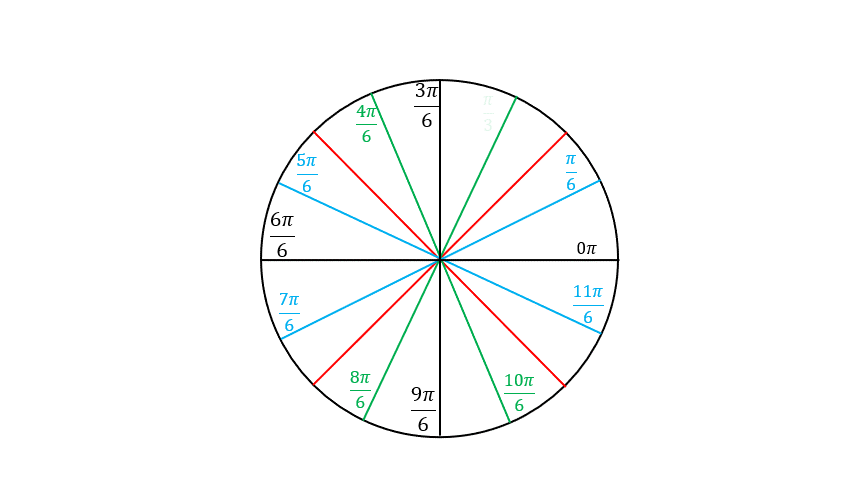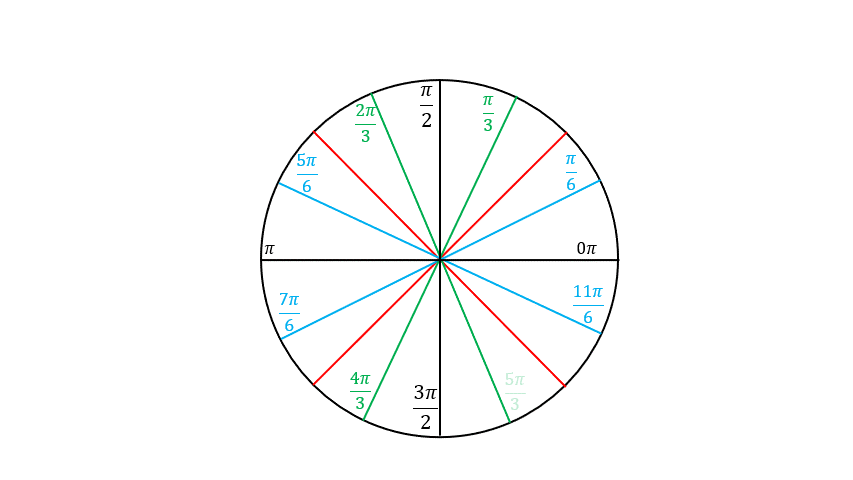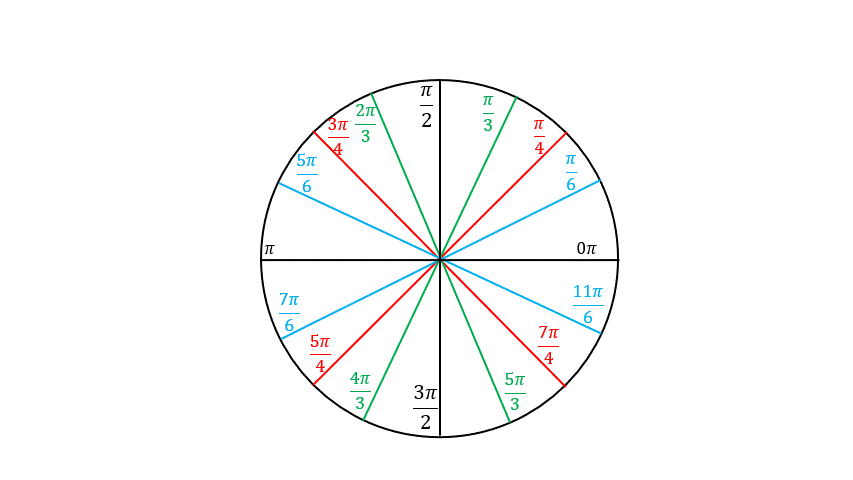
The coordinates