Section 4.1: Angles

Instructor Katherine Cliff

Join this presentation

https://precalcandtrig.net/lectures22/sec41angles.html

Warm Up Questions

Convert 34 inches into feet.
Given the similar triangles below, solve for \(x\).

plickers

Warm up 1

Convert 34 inches into feet.

A. \(\frac{6}{17}\) feet

B. \(\frac{17}{6}\) feet

C. 17 feet

D. 408 feet

Warm up 2

Given the similar triangles below, solve for \(x\).

A. 12.94

B. 37.4

C. 14.3

D. 0.077

Housekeeping

Homework due tomorrow (Friday)
Student Hours:
- Mondays and Wednesday from 11-noon
- Tuesdays and Thursdays from 2-3pm
- and Fridays from 9-11 am
PASS:
- Sundays 2 – 3:30 in Engineering 233 (the Math Center)
- Wednesdays 11 – 12:30 in Engineering 239

Housekeeping

Syllabus

Academic honesty

Constructing Angles

Constructing Angles: conventions

If we sweep the terminal side in the ________________ direction, we give the angle a ______________ value.
If we sweep the terminal side in the ________________ direction, we give the angle a ______________ value.

What the heck is a radian?

Converting from degrees to radians

Key fact:

So in general to convert from degrees to radians:

Example

Convert \(30^\circ\) to radians

Converting from radians to degrees

Example

Convert \(\frac{\pi}{4}\) to degrees

You try: convert

plickers

A. \(60^\circ\) to radians

B. \(\frac{3\pi}{2}\) to degrees

desmos.com/scientific

You try: convert

plickers

C. \(\frac{11\pi}{4}\) to degrees

D. \(460^\circ\) to radians

desmos.com/scientific

Coterminal Angles

Click here for interactive demo

Find the smallest, positive, coterminal angle.

plickers

A. \(800^\circ\)

B. \(-430^\circ\)

Find the smallest, positive, coterminal angle.

plickers

C. \(-\frac{13\pi}{6}\)

D. \(\frac{11\pi}{4}\)

Arc Length

Sector Area

Example: Find the arc length given the central angle and radius:

A. \(\theta = 27^\circ\), \(r = 2.5\) mm

Find the sector area given the central angle and radius:

B. \(\theta = 27^\circ\), \(r = 2.5\) mm

Example: Find the arc length given the central angle and radius:

C. \(\theta = \frac{\pi}{6}\), \(r = 6\) yd

Example: Find the sector area given the central angle and radius:

D. \(\theta = \frac{\pi}{6}\), \(r = 6\) yd

Warm up Day 2

Convert 528 feet per second into miles per hour.

Warm up 2

Convert 528 feet per second into miles per hour.

A. 46464 mph

B. 6 mph

C. 22809600 mph

D. 360 mph

Angular speed

Natalia’s angular speed describes how fast she’s spinning.
Measured in units like “revolutions per minutes” or “rotations per second”, etc.
- angle measure per time

Linear speed

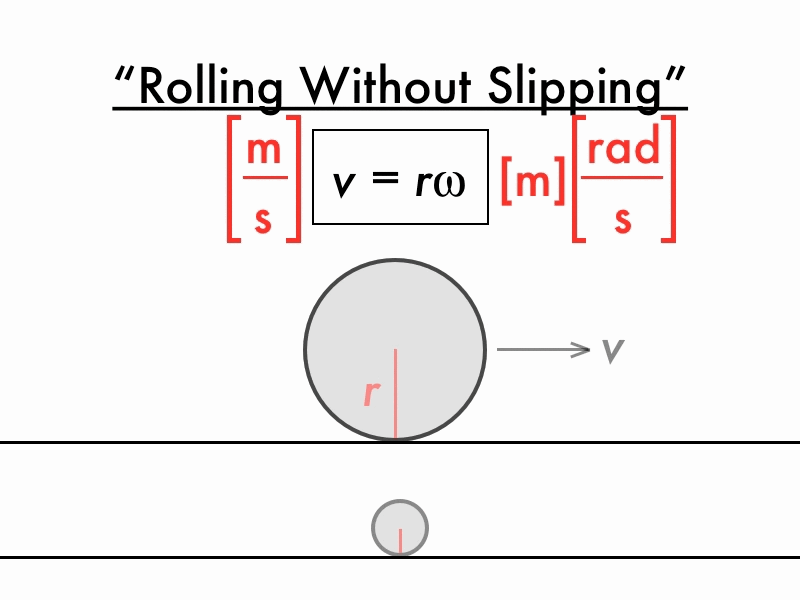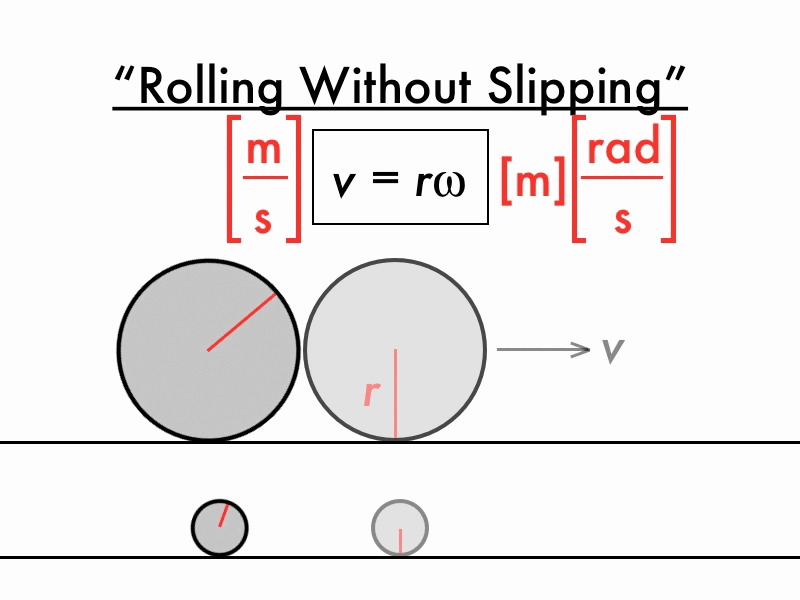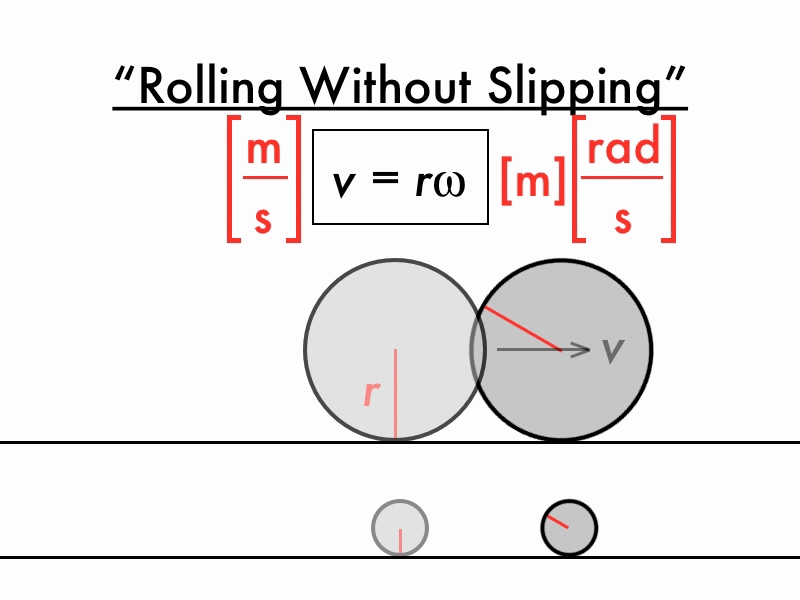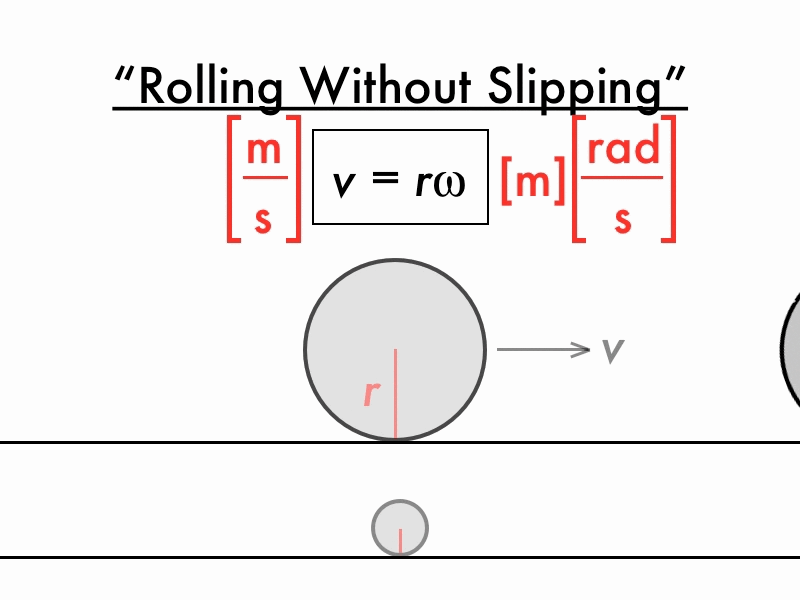
Linear speed describes how fast a spinning object is moving in a straight line.
Linear speed also describes how fast an object on the edge of our circle would travel if we suddenly let go.
- distance per time

How do angular and linear speed relate?

Big idea:

\[v = \omega r\]

v is linear speed (distance per time)
\(\omega\) (“omega”) is angular speed
- \(\omega\) must be in radians per time
r is radius
- radius units should match distance units in linear speed

Example

A bicycle with 24-inch diameter wheels is traveling at 15 mi/h. Find the angular speed of the wheels in rad/min. How many revolutions per minute do the wheels make?

Example

A car with 8.5 inch radius wheels is traveling at 25 ft/sec. How many revolutions per minute do the wheels make?

A car with 8.5 inch radius wheels is traveling at 25 ft/sec. How many revolutions per minute do the wheels make? Give your final answer accurate to 3 decimal places.

Example: A gear of radius 9 cm spins one revolution in 17 seconds. What is the angular velocity of the gear (in rad/sec)?

A speck of dust flings off the edge of the wheel. What is its linear velocity?

Example

A CD has diameter of 120 millimeters. When playing audio, the angular speed varies to keep the linear speed constant where the disc is being read. When reading along the outer edge of the disc, the angular speed is about 200 RPM (revolutions per minute). Find the linear speed. Give your answer accurate to two decimal places.