Right Triangle Trigonometry last day
Instructor Katherine Cliff
Inverse Trigonometric Functions
In a right triangle with reference angle \(\theta\)…
If \(\sin(\theta) = n\), then \(\sin^{-1}(n) = \theta\) or \(\arcsin(n)=\theta\).
If \(\cos(\theta) = n\), then \(\cos^{-1}(n) = \theta\) or \(\arccos(n)=\theta\).
If \(\tan(\theta) = n\), then \(\tan^{-1}(n) = \theta\) or \(\arctan(n)=\theta\).
Important Note about Reciprocal vs. Inverse Trig Functions
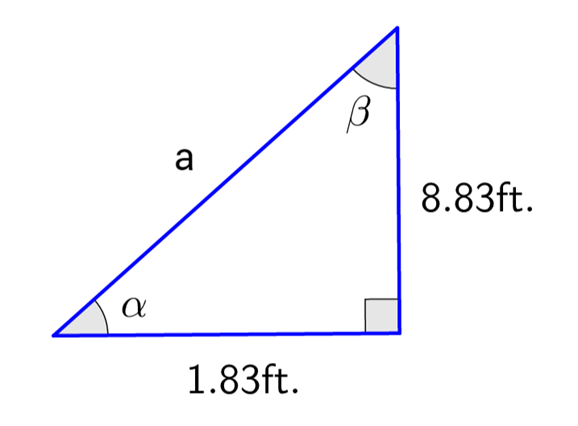
Example: Solve for \(\alpha\)
Example: Solve for \(\beta\)
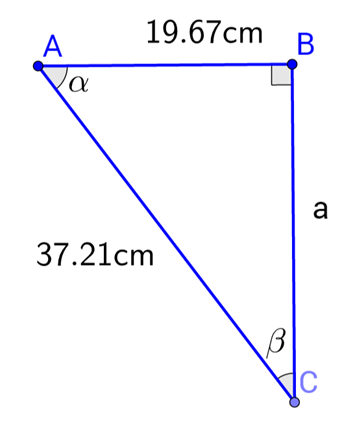
A. \(\arccos\left(\frac{19.67}{37.21}\right)\)
B. \(\arcsin\left(\frac{19.67}{37.21}\right)\)
C. \(\frac{1}{\sin\left(\frac{19.67}{37.21}\right)}\)
D. \(\frac{1}{\cos\left(\frac{19.67}{37.21}\right)}\)
Example: Solve for \(\alpha\)
Angles of elevation and depression
Example
The angle of depression from the top of a Building in New York to a point on the ground at a distance of 2 miles from the base of the building is found to be 5 degrees Using this information, find the height of the building.
Example
A radio tower is located 375 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is \(30^\circ\) and that the angle of depression to the bottom of the tower is \(26^\circ\) . How tall is the tower?