Right Triangle Trigonometry*

Instructor Katherine Cliff

Join this presen- tation

Warm Up Question:

Solve the equation for x:

\[\frac{2}{x} = 4\]

A. \(x = 2\)

B. \(x = \frac12\)

C. \(x = 4\)

D. \(x = 8\)

plickers

Warmup question 2

Which of the following expressions is not equivalent to the others?

A. \(\frac{-5+x}{-10x+x^2}\)

B. \(\frac{x-5}{x^2-10x}\)

C. \(\frac{1+x}{2x+x^2}\)

D. \(\frac{-5+x}{x(-10+x)}\)

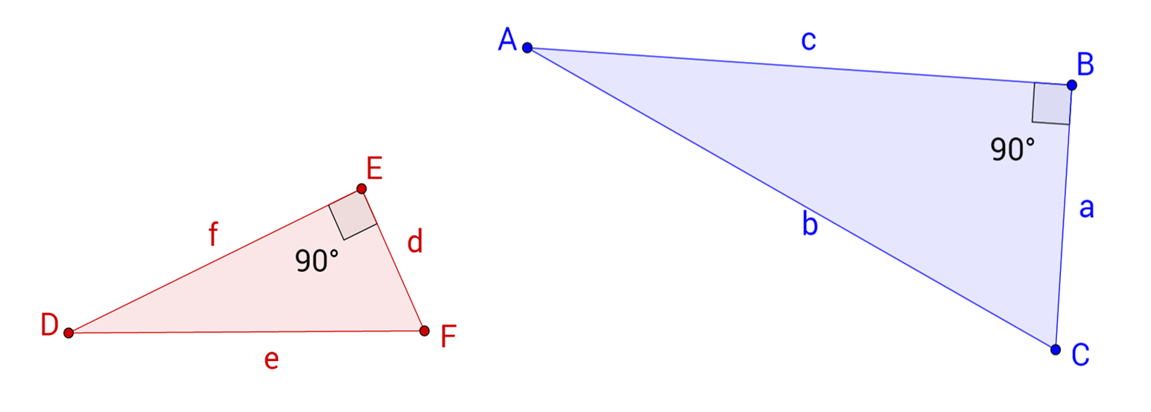
If I say that \(\triangle ABC\) is similar to \(\triangle DEF\), then what information can you tell me about the two triangles?

Similar Triangles

What is the minimum information we need to know that two triangles are similar?

In trigonometry, we’ll only work with right triangles (one angle is \(90^\circ\)). Then, we’ll typically work with one other angle in the triangle, creating a “class” of similar triangles.

Trigonometry means the study of triangles!

Trigonometric Ratios

Naming the sides of a right triangle with reference angle \(\theta\):






Example:

Name the sides of this triangle using the \(56^\circ\) angle as the reference angle: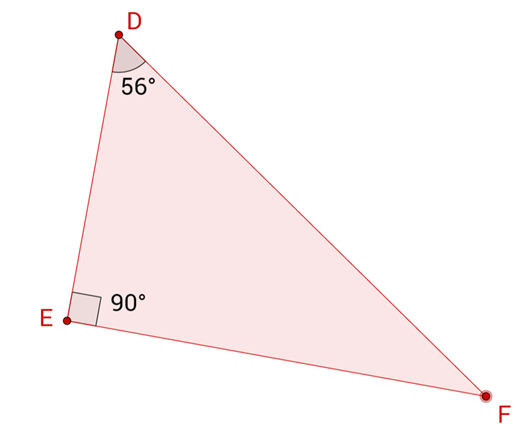

Trigonometric Ratios







Trigonometric Ratios

Memorization trick

Trigonometric Ratios

Notation note

Example:

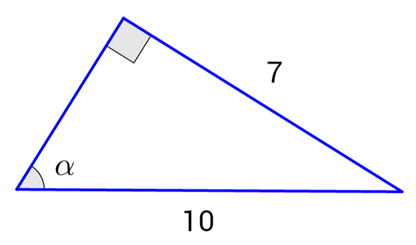
Calculate sin⁡(α), cos⁡(α), and tan⁡(α) given the following triangle:

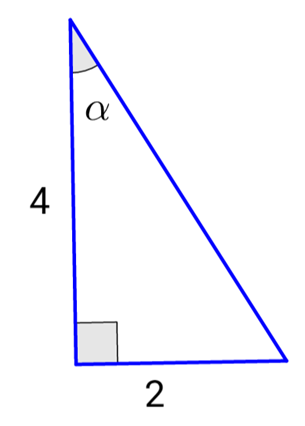
Example:

Calculate sin⁡(α), cos⁡(α), and tan⁡(α) given the following triangle:

plickers

Work on number 1 in your packet.

Consider the equilateral triangle pictured below:

What are the measures of the angles in this triangle? Label the two base angles with this measure.

What is the length of the base of this triangle?

Draw an altitude from the top vertex to the base of the triangle, and label it h. What will that altitude do to the top angle of the triangle? What will it do to the length of the base of the triangle? Use this information to label the triangle.

Now we’ve created two right triangles. Draw one of the triangles here, and use that triangle and the Pythagorean Theorem to solve for \(h\).

Special Right Triangle

Now we’ve created our first special right triangle, a \(30^\circ-60^\circ-90^\circ\) triangle. Use this triangle to find the sine and cosine of \(30^\circ\) and the sine and cosine of \(60^\circ\).

Special Right Triangle

Use what you’ve learned to find the sines and cosines of \(\frac{\pi}{6}\) and \(\frac{\pi}{3}\).

Now work on numbers 3 and 4 in the packet.

What are the measures of the non-right angles in this triangle? Label these two angles with this measure.

Solve for the length of the hypotenuse (using the Pythagorean Theorem). Label the triangle with this length.

Now we’ve created our second special right triangle, a \(45^\circ-45^\circ-90^\circ\) triangle. Use it to find the sine and cosine of \(45^\circ\).

Now use what you’ve learned to find the sine and cosine of \(\frac{\pi}{4}\).

Reciprocal Trigonometric Ratios







Important note about the reciprocal ratios!!!!

Example:

Calculate csc⁡(α), sec⁡(α), and cot⁡(α) given the following triangle:

Example:

Calculate csc⁡(α), sec⁡(α), and cot⁡(α) given the following triangle:

plickers

Using Right Triangle Trig to solve for missing information.

What do we do if we don’t have a special triangle?

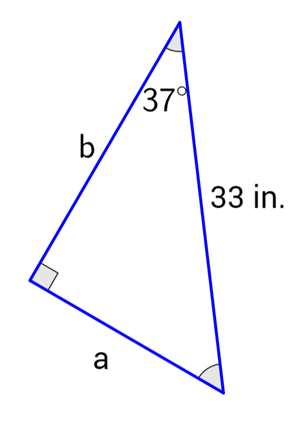
Example: Find the value of a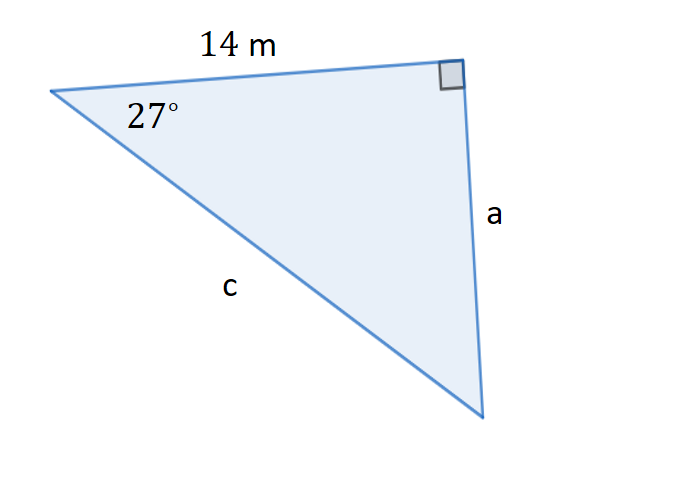

Example: Find the value of a

plickers

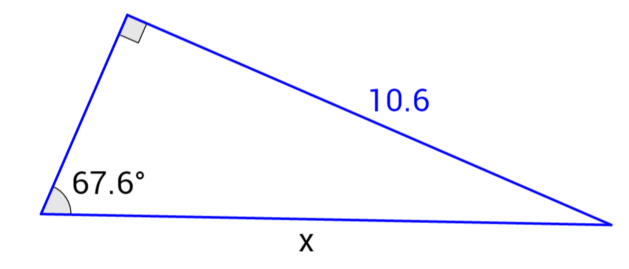
Example: Find the value of x

plickers

Inverse Trigonometric Functions

  • If \(\sin(\theta) = n\), then \(\sin^{-1}(n) = \theta\) or \(\arcsin(n)=\theta\).



  • If \(\cos(\theta) = n\), then \(\cos^{-1}(n) = \theta\) or \(\arccos(n)=\theta\).



  • If \(\tan(\theta) = n\), then \(\tan^{-1}(n) = \theta\) or \(\arctan(n)=\theta\).



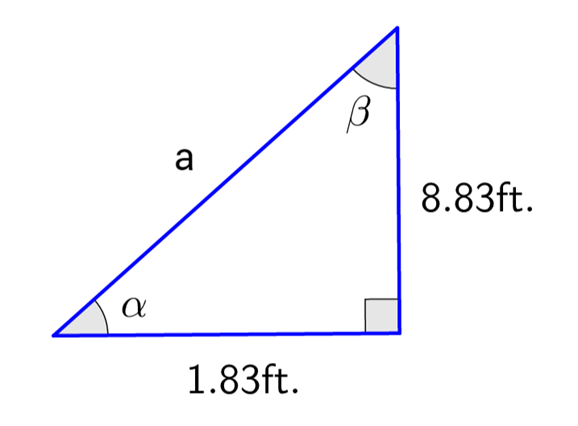
Example: Solve for \(\alpha\)

Example: Solve for \(\beta\)

plickers




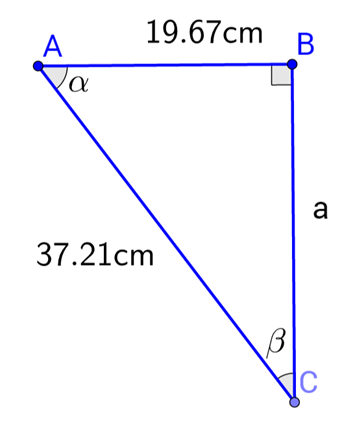
A. \(\arccos\left(\frac{19.67}{37.21}\right)\)

B. \(\arcsin\left(\frac{19.67}{37.21}\right)\)

C. \(\frac{1}{\sin\left(\frac{19.67}{37.21}\right)}\)

D. \(\frac{1}{\cos\left(\frac{19.67}{37.21}\right)}\)

Example: Solve for \(\alpha\)

plickers